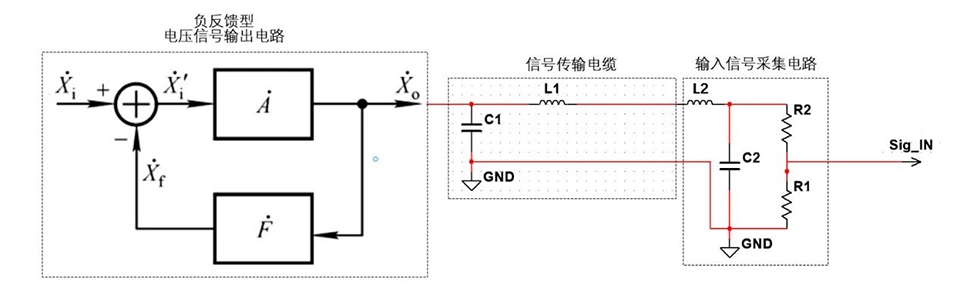
如图1，电压源信号的传输主要由3部分组成：
- 负反馈型电压信号输出电路。
- 信号传输电缆。其中，C1、L1为电缆的寄生电容和寄生电感，其参数和电缆长度、布线型式等有直接关系。
- 输入信号采集电路。其中，L2、C2为部分采样电路可能布置的低通滤波电路。
对于负反馈型电压信号输出电路，其输入信号的计算公式如下：
∣Xi′∣=∣Xi∣−∣Xf∣
当∣Xf∣的相位超期或滞后180°时，输入信号的计算公式就变成了如下形式：
∣Xi′∣=∣Xi∣+∣Xf∣
也就是说，在没有输入信号(∣Xi∣为0)的情况下，反馈信号(∣Xf∣)维持输出信号(|X0|),输出信号(|X0|)又反过来维持反馈信号(∣Xf∣)。此时，自激振荡就形成了。
总而言之，如下2个条件，是导致自激振荡的前提：
- |AF| > 1
- φA+φF=(2n+1)Π
回路上的相位差从何而来呢？
信号传输电缆上寄生的C1、L1，输入信号采集电路上的L2、C2，以及信号输出电路上的滤波电容都有可能导致提前或滞后的相位差。最终的相位差是这些相位差之和，如果超期或滞后180°，就有可能自激振荡。
如何避免自激振荡呢？
我们只需要确保在应用频域的范围内，前述2个条件不能被同时满足，就可以避免自激振荡了。
如图2：
f c为环路增益20log|AF|降到0dB的频率。
f o为环路相位差小于-180°的频率。
所以，当相位差超期或滞后180°时，环路的增益降到0以下，电路就是稳定的。
相对来说，电流源信号为什么不容易产生振荡？
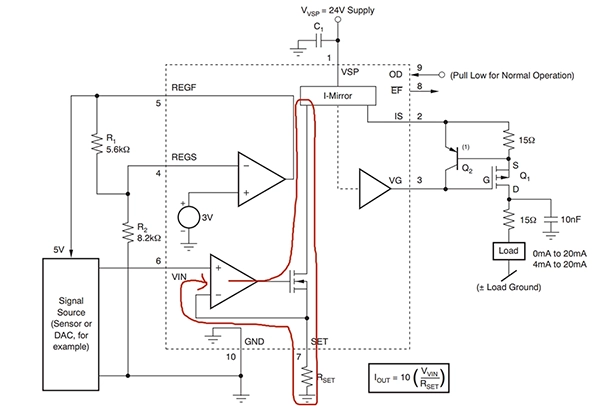
如图2所示，目前应用比较广泛的电流源输出为镜像电流源。它的负反馈调节回路只包含红线所标识的镜像电流源的一侧。所以，外部的负载电路对反馈回路的相位差和增益影响小，只要控制好内部反馈回路的参数，就不会发生振荡。
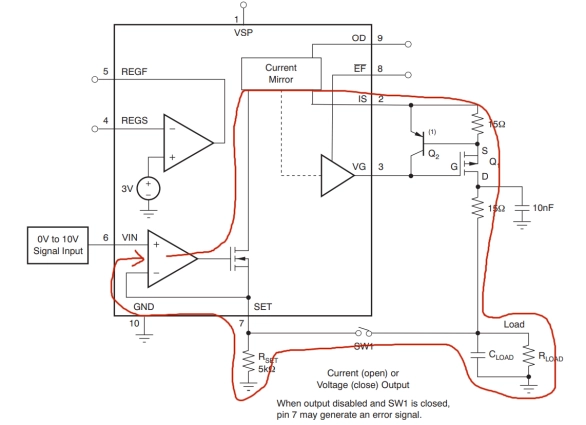
如图3所示，电压源信号的反馈点位于电路输出点。所以，反馈回路包含红线所标示的内部电路和外部的电缆及采样电路。这样，当外部电缆或采样电缆的电气参数发生变化时，负反馈回路的相位差和增益也会发生变化。当这种变化使自激振荡的2个条件被满足时，就发生振荡了。
鄂公网安备 42018502006527号